Notes on Select Best Tasks for Cognitive Sub-Domain

Author

Zhang, Liang

Published

November 1, 2023

Modified

July 20, 2024

Code 
devtools::load_all()
# the identifiers are large integers
requireNamespace("bit64")
requireNamespace("parameters")

projects <- targets::tar_config_yaml()

最佳因子模型

我们采用了基于自助法（bootstrap）的因子聚类方法探索任务的因子归类。不过在开始之前，一些特别类似范式的任务仅保留了一个，如 表 1，其中thin一列为TRUE的是被去掉的任务。以下用all表示使用全部任务，用thin表示去掉类似范式任务的结果。

Code 
read_tsv("config/games_thin.tsv", show_col_types = FALSE) |>
  filter(!is.na(same_id)) |>
  mutate(thin = if_else(thin, "是", "否")) |>
  select(same_id, 名称 = game_name, 是否去掉 = thin) |>
  arrange(same_id, 是否去掉) |>
  gt::gt(
    groupname_col = "same_id",
    row_group_as_column = TRUE
  ) |>
  gtExtras::gt_highlight_rows(
    rows = 是否去掉 == "是",
    fill = "gray"
  )
表 1: 相似任务保留情况
名称 是否去掉
1 格子卡片 否
美术卡片 是
魔术师终极 是
数字卡片PRO 是
文字卡片 是
2 方向检测 否
色彩检测 是
3 注意指向 否
太空飞船PRO 是
注意警觉 是
4 速算师（中级） 否
专注大师_中级 是
5 宇宙黑洞A 否
城市导航 是
6 图形折叠 否
平面展开 是
7 三维心理旋转测试A 否
物体旋转 是
8 语义判断 否
词语判断 是
声调判断 是

由于因子个数对于我们的研究很重要，我们尝试了很多传统办法，结果很不稳定：

Code 
targets::tar_read(
  n_factors_test_all,
  store = projects$explore_factors$store
) |>
  plot()

targets::tar_read(
  n_factors_test_thin,
  store = projects$explore_factors$store
) |>
  plot()
(a) 包含全部任务
(b) 去除同范式任务
图 1: 传统方法的因子个数结果

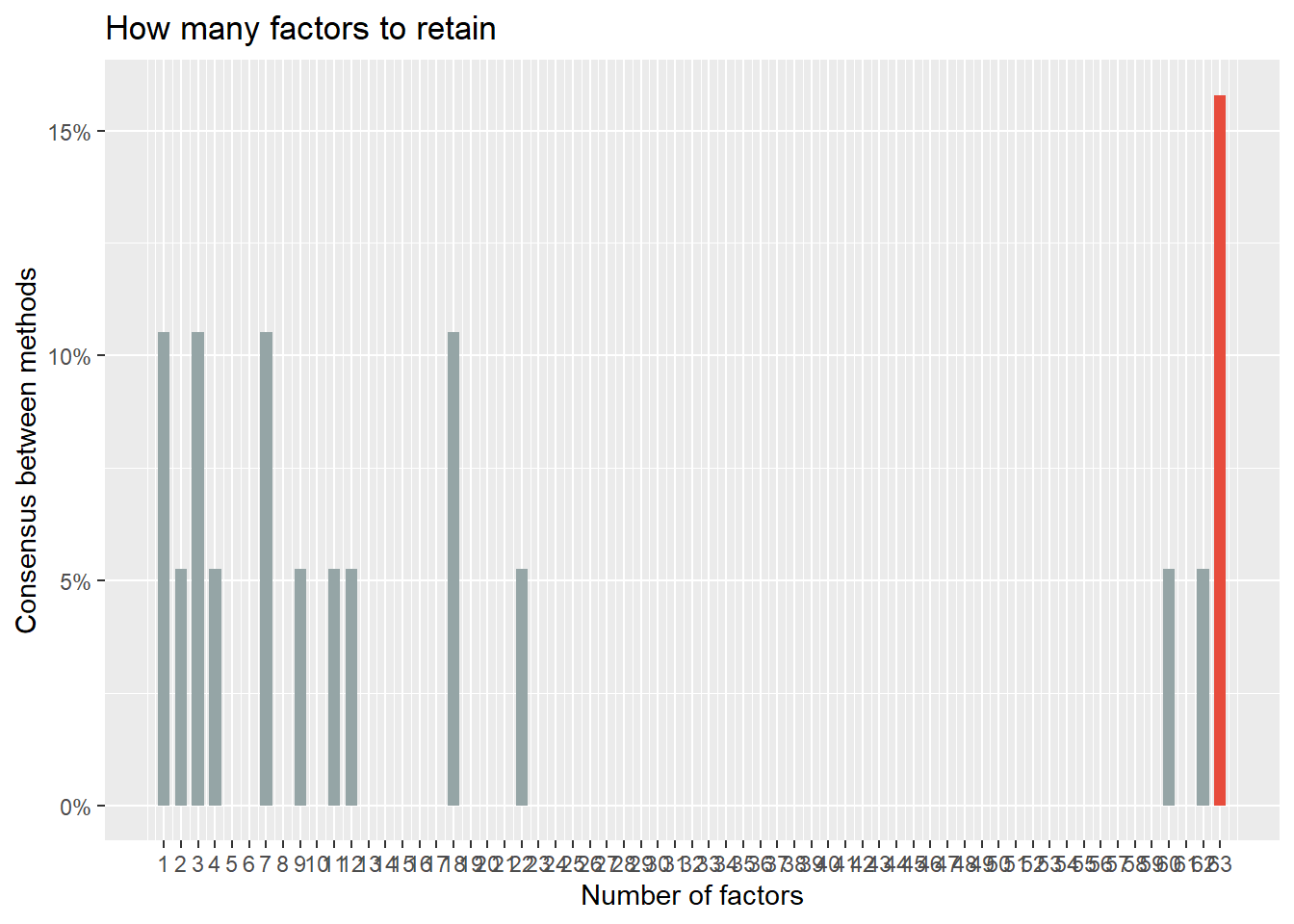
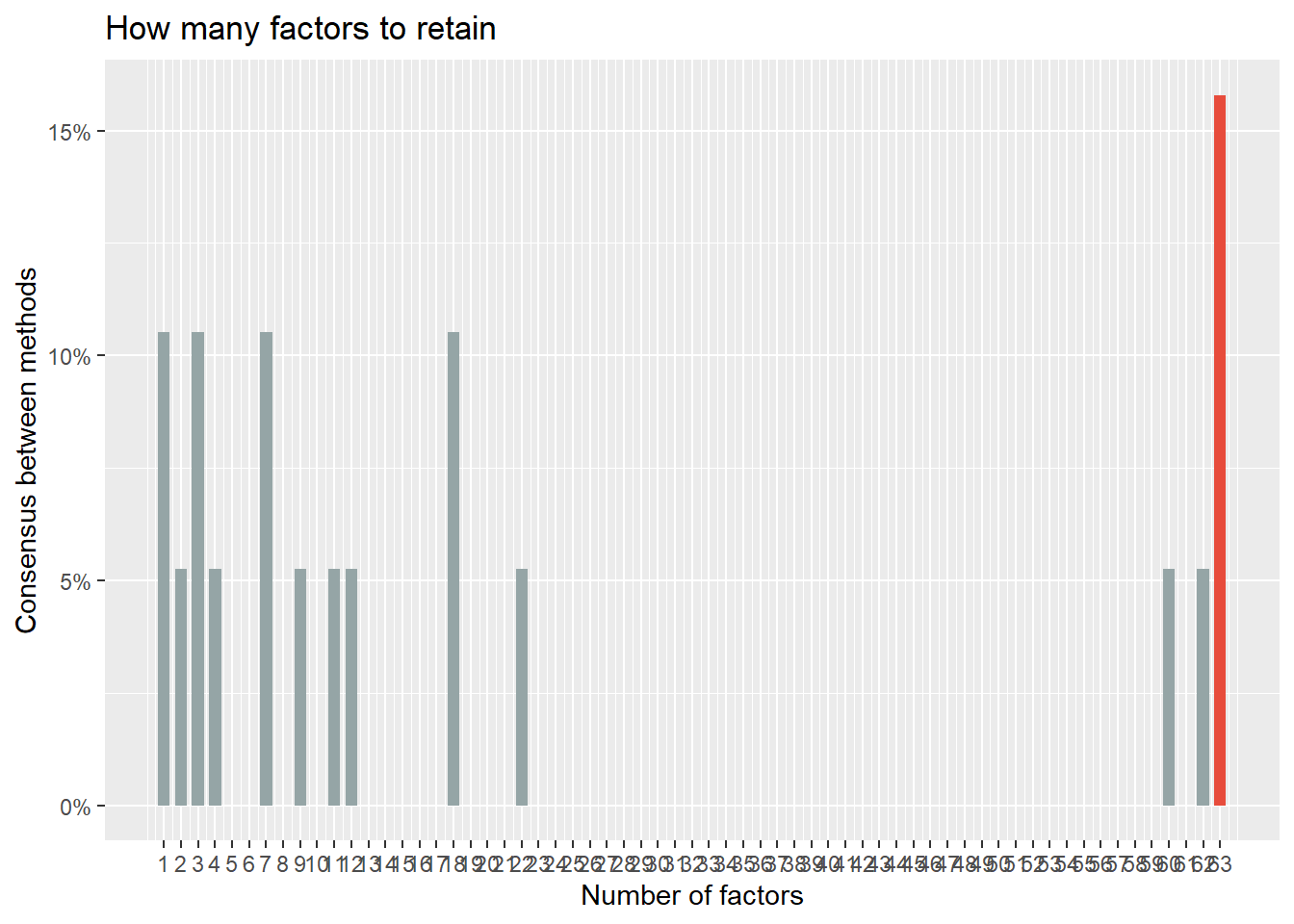
采用基于自助法的因子聚类方法，结果如 图 2。

Code 
targets::tar_read(cluster_stats, store = projects$explore_factors$store) |>
  ggplot(aes(n_fact, k, fill = crit)) +
  geom_raster() +
  geom_point(aes(n_fact, nc), color = "white") +
  facet_wrap(~schema) +
  scale_x_continuous(name = "Number of Factors", expand = c(0, 0)) +
  scale_y_continuous(name = "Number of Clusters", expand = c(0, 0)) +
  scale_fill_viridis_c(
    name = "Silhouette Score",
    breaks = scales::breaks_pretty(n = 4)
  ) +
  theme_minimal(base_size = 16) +
  theme(legend.position = "top") +
  coord_fixed()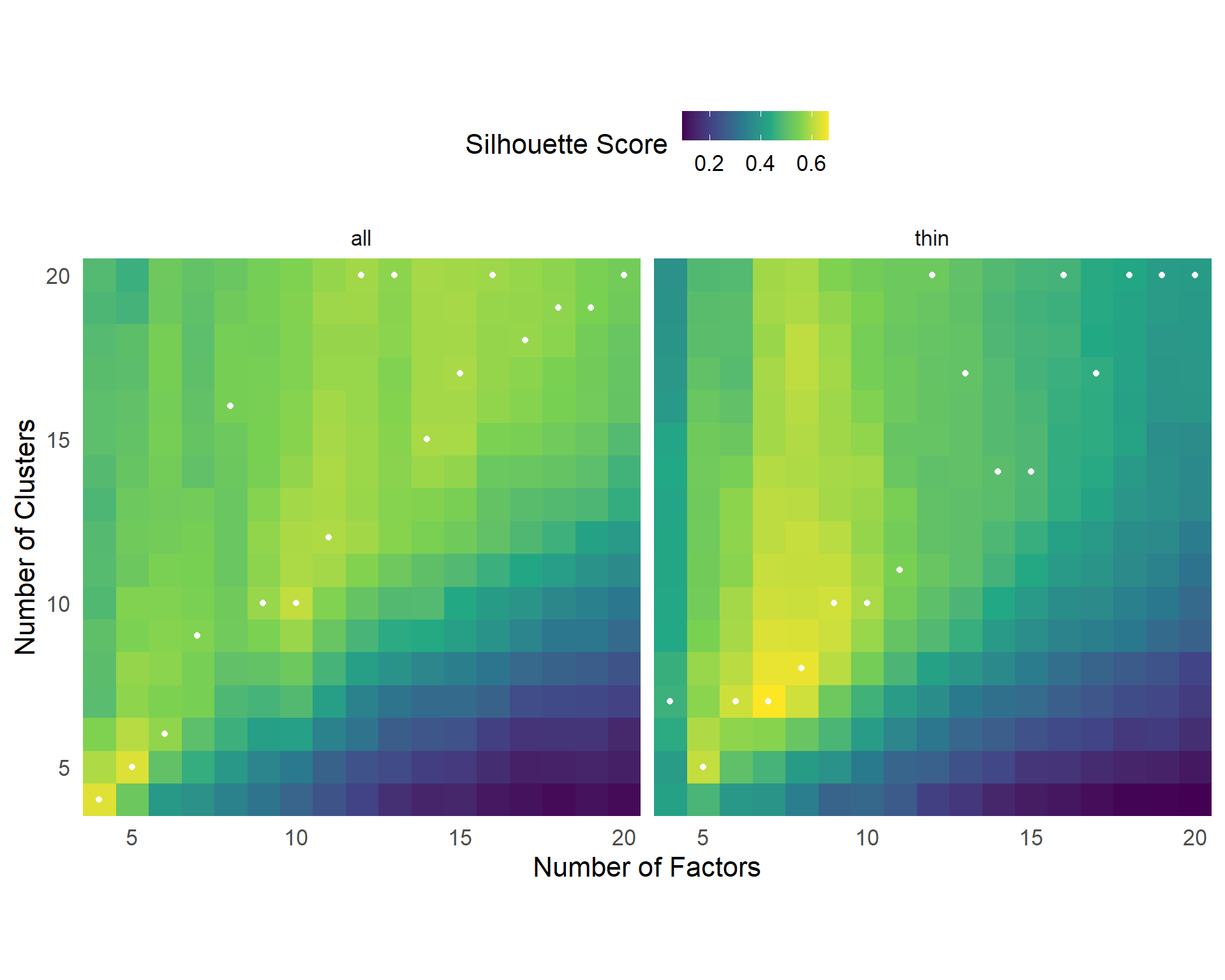
图 2: Evaluation of clustering results

我们将每种因子个数条件的最佳聚类结果进一步用验证性因子分析确定哪个模型最佳。注意，我们可以得到每个任务指标的轮廓系数（silhouette score），并且可以用此系数来确定该任务归入对应类别的可信度。一般而言，轮廓系数大于0.51时才可靠。同时，为了保证因子分析结果的可比性，我们将轮廓系数不达标的的任务指标的载荷固定为0后做验证性因素分析。注意这样也会导致一些聚类结果中部分因子的所有成分指标载荷为0，从而导致模型不能成功拟合，也说明这种聚类结果的不可靠。

Code 
tar_load(
  c(gofs, cluster_stats),
  store = projects$explore_factors$store
)
stats <- cluster_stats |>
  filter(k == nc) |>
  full_join(gofs, by = c("schema", "n_fact"))

measures <- c("crit", "bic", "cfi", "rmsea")
for (measure in measures) {
  p <- stats |>
    filter(!is.na(.data[[measure]])) |>
    ggplot(aes(n_fact, .data[[measure]])) +
    geom_point() +
    geom_line() +
    scale_x_continuous(
      name = "Number of Factors",
      breaks = scales::breaks_width(1)
    ) +
    facet_wrap(~ schema, scales = "free_y") +
    ggpubr::theme_pubclean()
  print(p)
}
(a) Mean Silhouette Score
(b) BIC
(c) CFI
(d) RMSEA
图 3: 所有聚类模型拟合情况（仅展示成功拟合的模型）

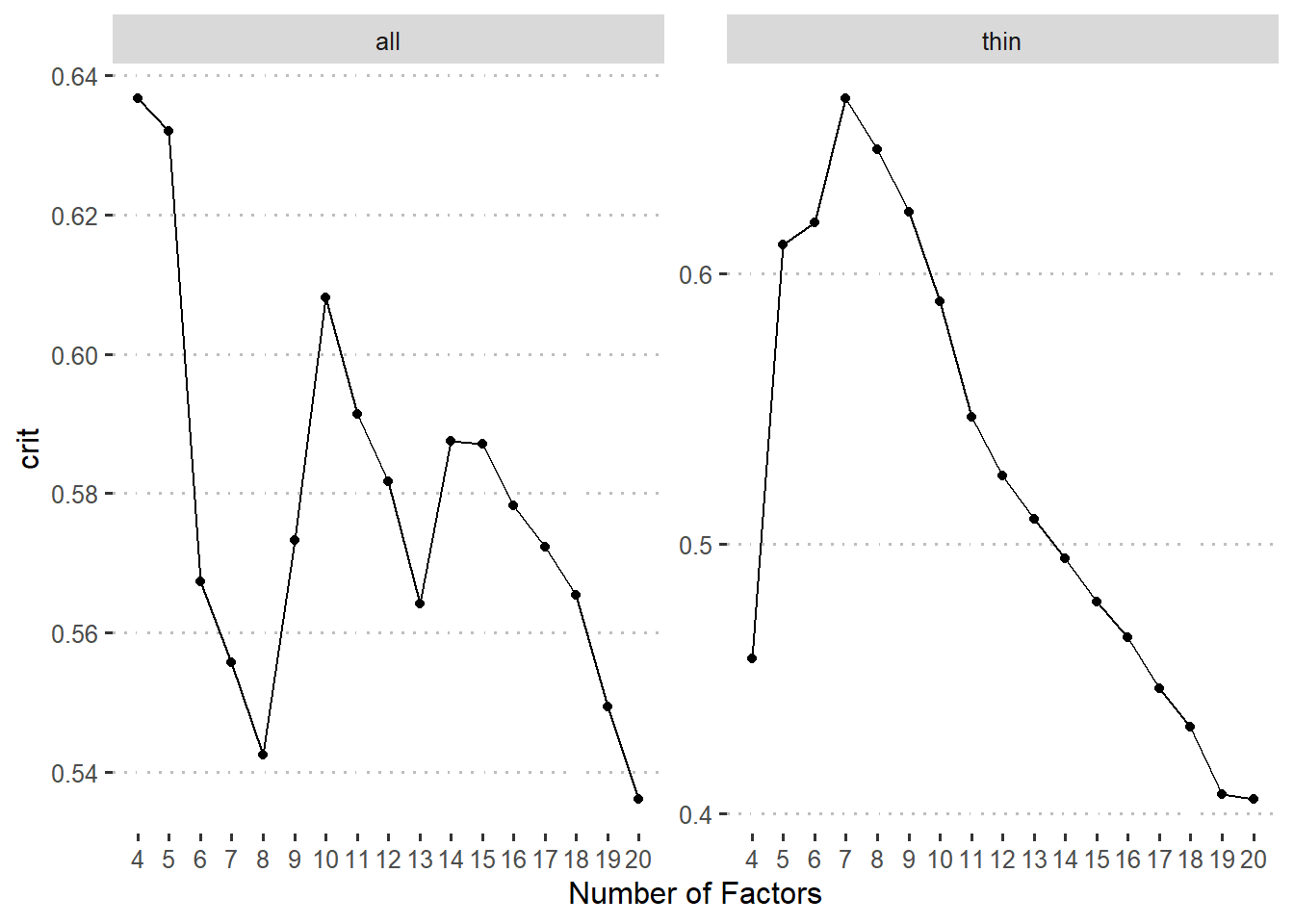
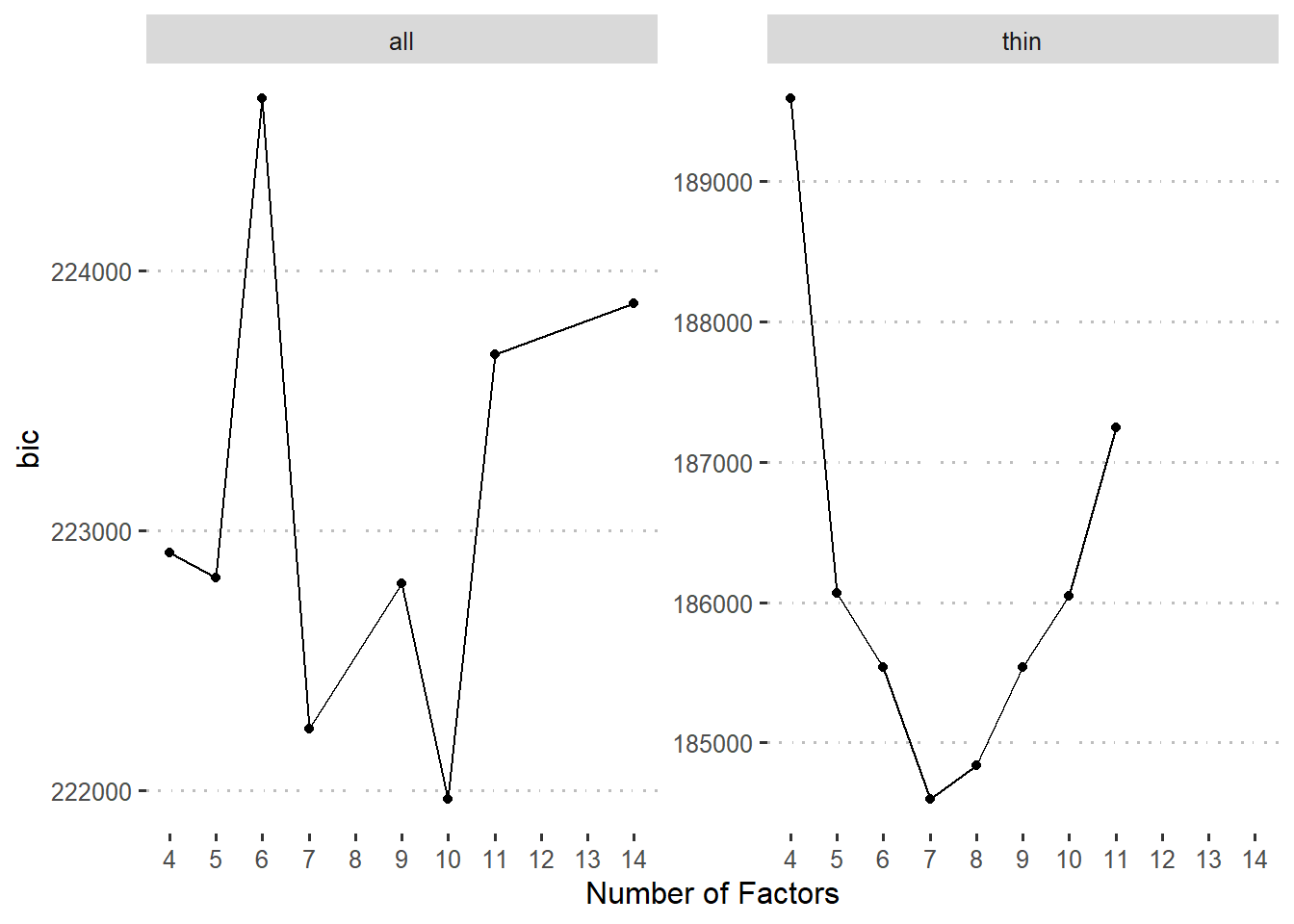
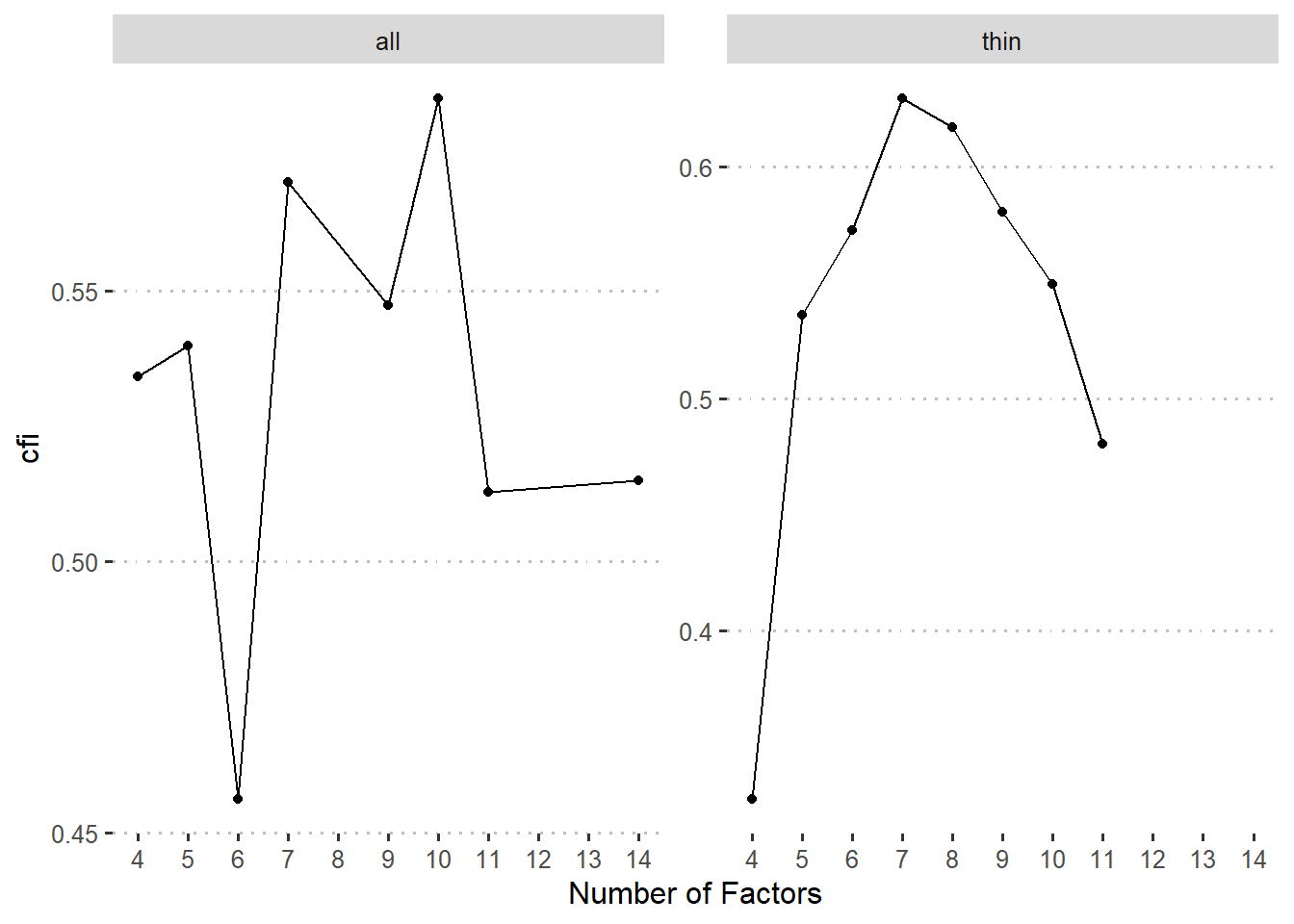
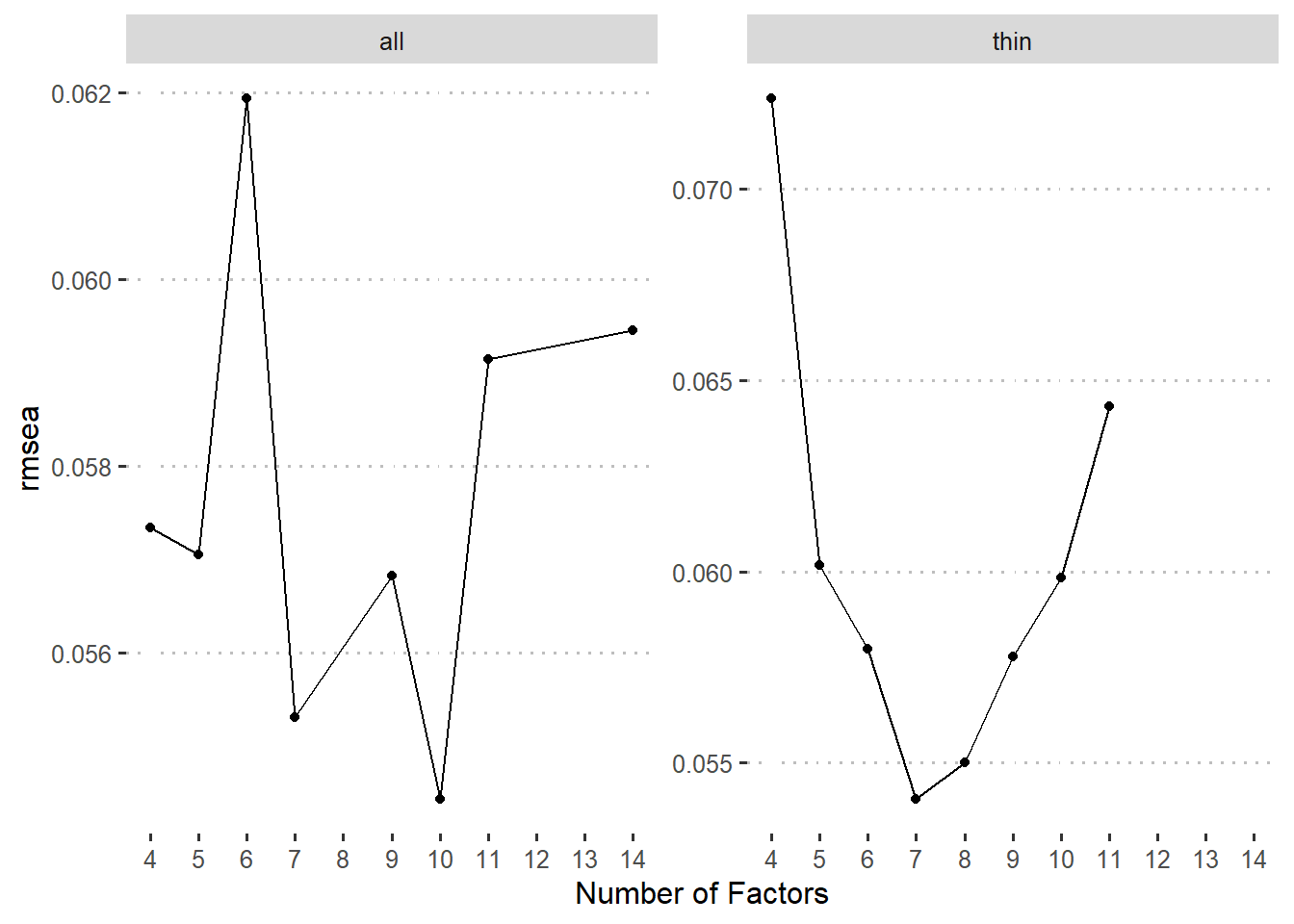
进一步，根据Vuong (1989)提出的比较非嵌套模型的检验，我们也对拟合成功的模型做了两两比较。

Code 
targets::tar_read(comparison, store = projects$explore_factors$store) |>
  select(left, right, everything()) |>
  arrange(right) |>
  gt::gt(groupname_col = "schema", row_group_as_column = TRUE) |>
  gt::fmt_number(columns = !c(left, right))
left right omega p_omega p_left_better p_right_better
all 5 4 5.37 0.00 0.20 0.80
6 4 8.82 0.00 1.00 0.00
10 4 6.92 0.00 0.00 1.00
6 5 5.75 0.00 1.00 0.00
10 5 7.43 0.00 0.00 1.00
10 6 9.71 0.00 0.00 1.00
thin 6 5 1.47 0.00 0.00 1.00
7 5 3.88 0.00 0.00 1.00
8 5 4.30 0.00 0.00 1.00
7 6 2.31 0.00 0.00 1.00
8 6 2.85 0.00 0.00 1.00
8 7 0.99 0.00 1.00 0.00

基于此结果我们可以比较确定地指出我们的数据可以很好地拟合一个包含七个或者八个因子的模型，同时，对比这两个模型发现的区别在于有没有视觉搜索类任务作为单独的成分。而根据简约原则，当两个模型没差异的时候，应选择更简单的模型，此处我们选择了七因子模型作为最终模型。此模型各个因子具体结果如 图 4 。根据每一个因子里面包含任务之间的关系，我们也给出这些因子的名字。

Code 
withr::local_seed(123) # ensure wordcloud reproducible
dimensions <- read_csv("config/dimensions.csv", show_col_types = FALSE)
targets::tar_read(config_thin_7, store = projects$explore_factors$store) |>
  left_join(dimensions, by = "cluster") |>
  separate_wider_delim(
    observed, ".",
    names = c("game_name_abbr", "index_name")
  ) |>
  mutate(
    dim_name = fct_reorder(dim_name, cluster),
    game_name = data.iquizoo::match_info(game_name_abbr, to = "game_name"),
  ) |>
  ggplot(aes(label = game_name, size = sil_width, color = sil_width < 0.5)) +
  ggwordcloud::geom_text_wordcloud() +
  scale_color_grey() +
  facet_wrap(~dim_name) +
  theme_minimal()
图 4: 最佳模型各因子所含任务指标

任务挑选

图 5 给出了各种方案不同模型的拟合优度。整体上看，基于载荷或者轮廓系数选出的任务都能得到相对较好的CFI拟合指标（>0.9）。

Code 
tar_read(gofs, store = projects$confirm_factors$store) |>
  mutate(
    name = factor(name, hypers_config_dims$name),
    group = case_match(
      name,
      c("thresh_sil_050", "thresh_sil_070") ~ "thresh_sil",
      c("thresh_load_030", "thresh_load_040") ~ "thresh_load",
      c("top_sil_3", "top_sil_4") ~ "top_sil",
      c("top_load_3", "top_load_4") ~ "top_load",
      .default = name
    ),
    .after = name
  ) |>
  ggplot(aes(name, cfi, color = theory)) +
  geom_point() +
  geom_line(aes(group = theory)) +
  facet_grid(cols = vars(group), space = "free", scales = "free_x") +
  scale_x_discrete(name = NULL) +
  ggpubr::theme_pubclean() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))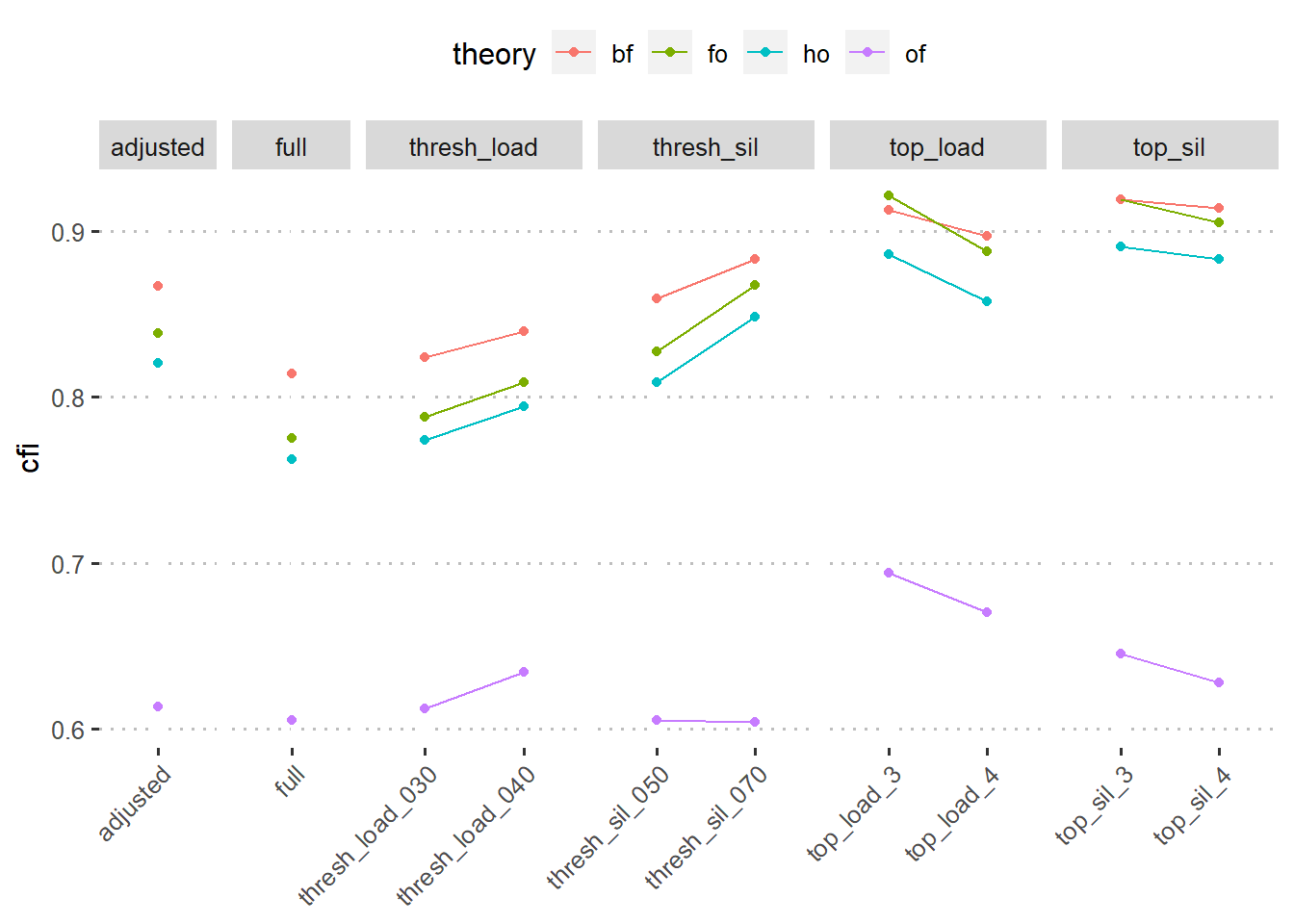
图 5: 不同方案CFI拟合优度

表 2 展示了每个维度所有任务指标的载荷。

Code 
targets::tar_read(fit_fo_full, store = projects$confirm_factors$store) |>
  parameters::model_parameters(component = "loading") |>
  as_tibble() |>
  separate_wider_delim(
    From, ".",
    names = c("game_name_abbr", "index_name")
  ) |>
  left_join(data.iquizoo::game_info, by = "game_name_abbr") |>
  left_join(
    targets::tar_read(
      test_retest,
      store = projects$prepare_source_data_retest$store
    ) |>
      filter(origin == "rm_out"),
    by = join_by(game_id, index_name)
  ) |>
  mutate(Dimension = as_factor(match_dim_label(To))) |>
  select(
    Dimension,
    `Game Name` = game_name,
    `Index Name` = index_name,
    Loading = Coefficient,
    ICC = icc
  ) |>
  arrange(Dimension, desc(Loading)) |>
  gt::gt(
    groupname_col = "Dimension",
    row_group_as_column = TRUE
  )
表 2: 因子载荷
Game Name Index Name Loading ICC
Att_Spd 快速归类PRO ies 0.6787400 0.5946463
一心二用PRO nc 0.6365838 0.5032728
变戏法 ies 0.6026617 0.5200595
语义判断 nc 0.5896901 0.5044480
火眼金睛 nc 0.5428395 0.6036382
小狗回家 mean_score 0.5370434 0.6061863
我是大厨 score_total 0.5258004 0.2392425
雪花收藏家 nc_cor 0.4570217 0.4938276
连点成画PRO nc 0.4137019 0.5265635
舒尔特方格（中级） nc_cor 0.4071475 0.5584472
方向临摹 mean_log_err 0.2732702 0.5898830
WM_Rsn 三维心理旋转测试A nc 0.6967490 0.7091315
图形折叠 nc 0.6756488 0.6860115
图形推理 nc 0.6338678 0.4941794
格子卡片 dprime 0.6229752 0.6359423
视角判断 nc 0.5820512 0.5800200
数字推理 nc 0.5419078 0.5674540
登陆月球（中级） mean_log_err 0.5412515 0.6128001
按图索骥 mean_log_err_both 0.5230278 0.4900597
文字推理 nc 0.4440368 0.6123835
阅读判断 nc 0.3738147 0.5144023
各得其所 prop_perfect 0.2984172 0.3253265
强化学习 pc_test 0.2794045 0.2940566
Inh 候鸟迁徙PRO cong_eff_ies 0.5860210 0.6953626
数感 w 0.5171687 0.7042378
捉虫高级简版 dprime 0.5022757 0.3996592
方向检测 k 0.4988380 0.3174755
超级秒表PRO mrt 0.4702009 0.4749019
时间顺序判断 thresh_last_block 0.4696923 0.5801377
节奏感知 thresh_last_block 0.4524709 0.4337349
塔罗牌 nc 0.4454639 0.4520436
变色魔块PRO ssrt 0.3837396 0.5516098
多彩文字PRO cong_eff_ies 0.3765596 0.5645885
卡片分类PRO switch_cost_ies 0.3056030 0.4687936
言语记忆A fm_dprime 0.2257133 0.0000000
注意指向 cong_eff_ies 0.2063205 0.6606258
VSTM 幸运小球PRO nc 0.6706127 0.5658720
密码箱 nc 0.6367052 0.4504140
井然有序 nc 0.6244655 0.4969166
顺背数PRO nc 0.6010638 0.6340612
速算师（中级） nc 0.5152828 0.7844297
远距离联想 nc 0.3806711 0.5176199
时长分辨 thresh_last_block 0.3017391 0.5601665
SSTM 蝴蝶照相机 nc 0.7549573 0.6622464
位置记忆PRO nc 0.7000238 0.6388553
打靶场 nc 0.6434684 0.4946694
路径学习 nc 0.5407346 0.3010715
萤火虫PRO nc 0.4980568 0.5986120
EM 万花筒 nc 0.6299532 0.6092568
词汇学习 nc 0.6148498 0.3723588
过目不忘PRO nc 0.6075529 0.6004452
欢乐餐厅PRO nc 0.6051290 0.5162227
社交达人 fntotal 0.5727646 0.4827007
宇宙黑洞A nc 0.5516628 0.6075916
人工语言-高级 nc 0.5336025 0.2651027
事件记忆 nc 0.5304998 0.5468560
图片记忆A bps_score 0.4923994 0.4905354
连续再认PRO dprime 0.4866025 0.6425060
视觉记忆测试 nc 0.4761503 0.6060116
Shift 察颜观色PRO switch_cost_ies 0.5450219 0.5667099
多变计数师 switch_cost_ies 0.5435840 0.4726218
随机应变 switch_cost_ies 0.5356438 0.5841394
候鸟迁徙PRO switch_cost_ies 0.3728003 0.4911534

能力分估计（因子得分）

Code 
tar_load(scores_factor, store = projects$confirm_factors$store)
latents <- names(scores_factor)[-c(1:3)]
for (latent in latents) {
  p <- scores_factor |>
    filter(theory == "bf") |>
    pivot_wider(
      id_cols = user_id,
      names_from = name,
      values_from = all_of(latent)
    ) |>
    select(!user_id) |>
    GGally::ggpairs() +
    ggtitle(match_dim_label(latent))
  print(p)
}
图 6: 不同任务选择方案的因子得分相关

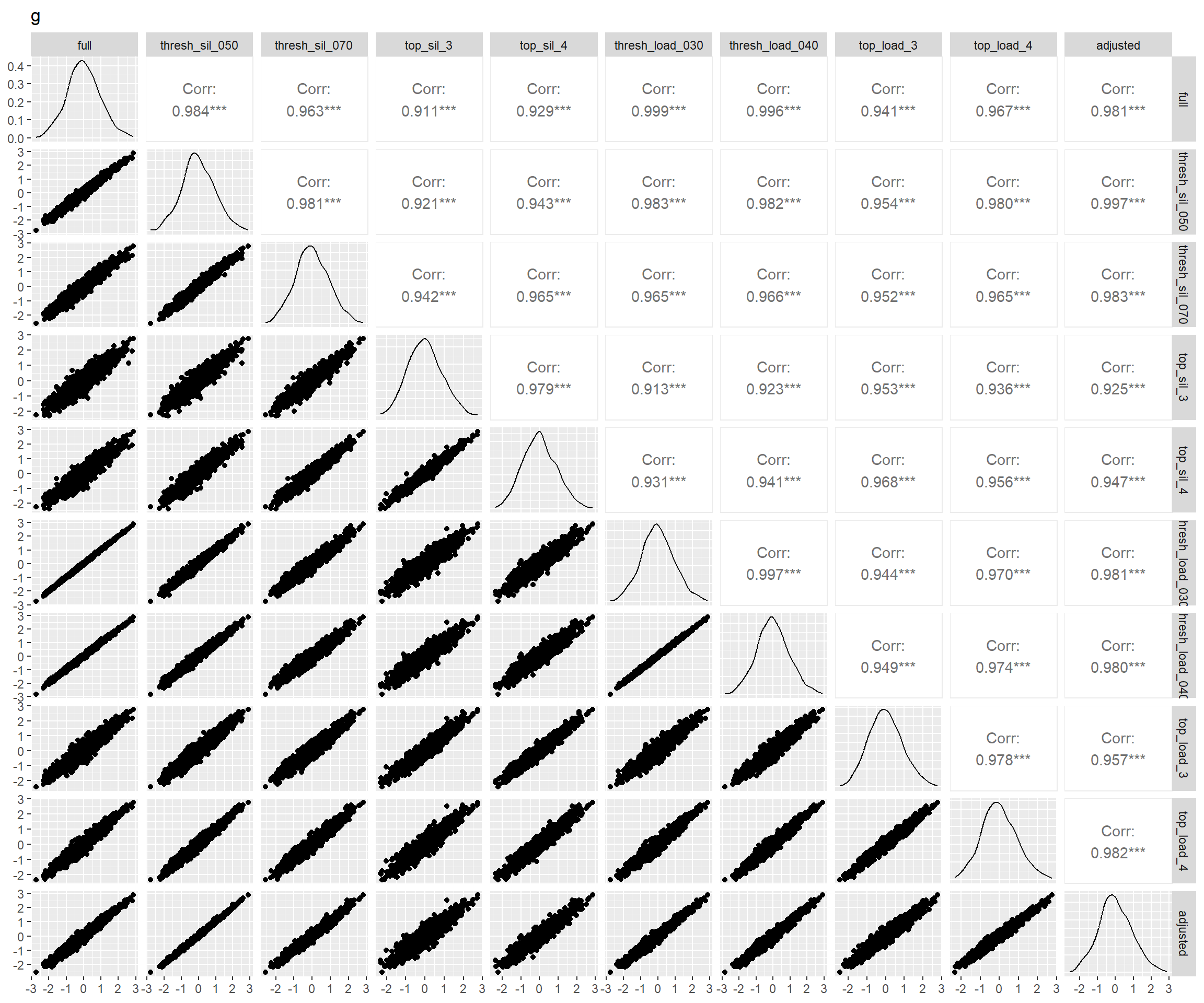
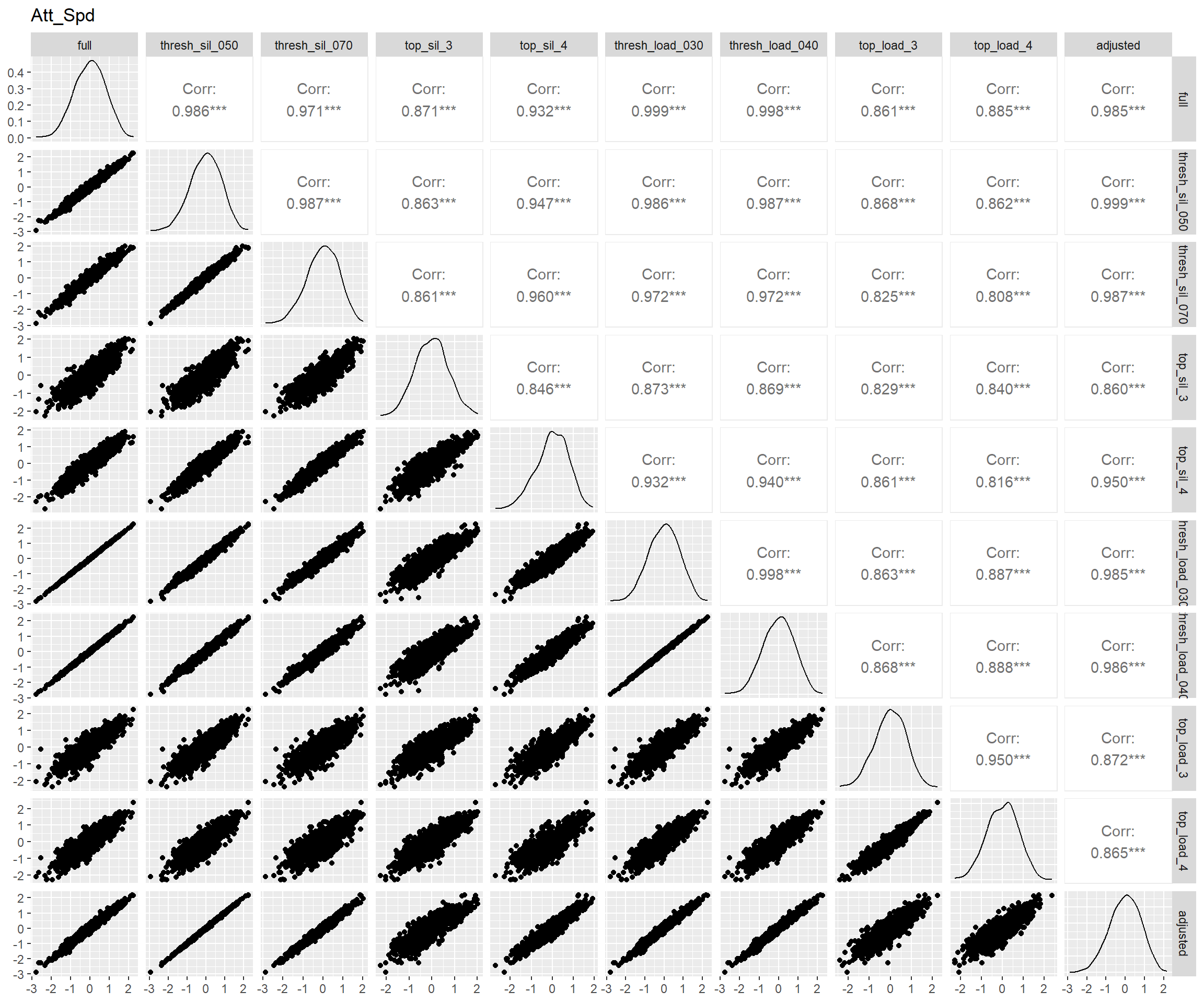
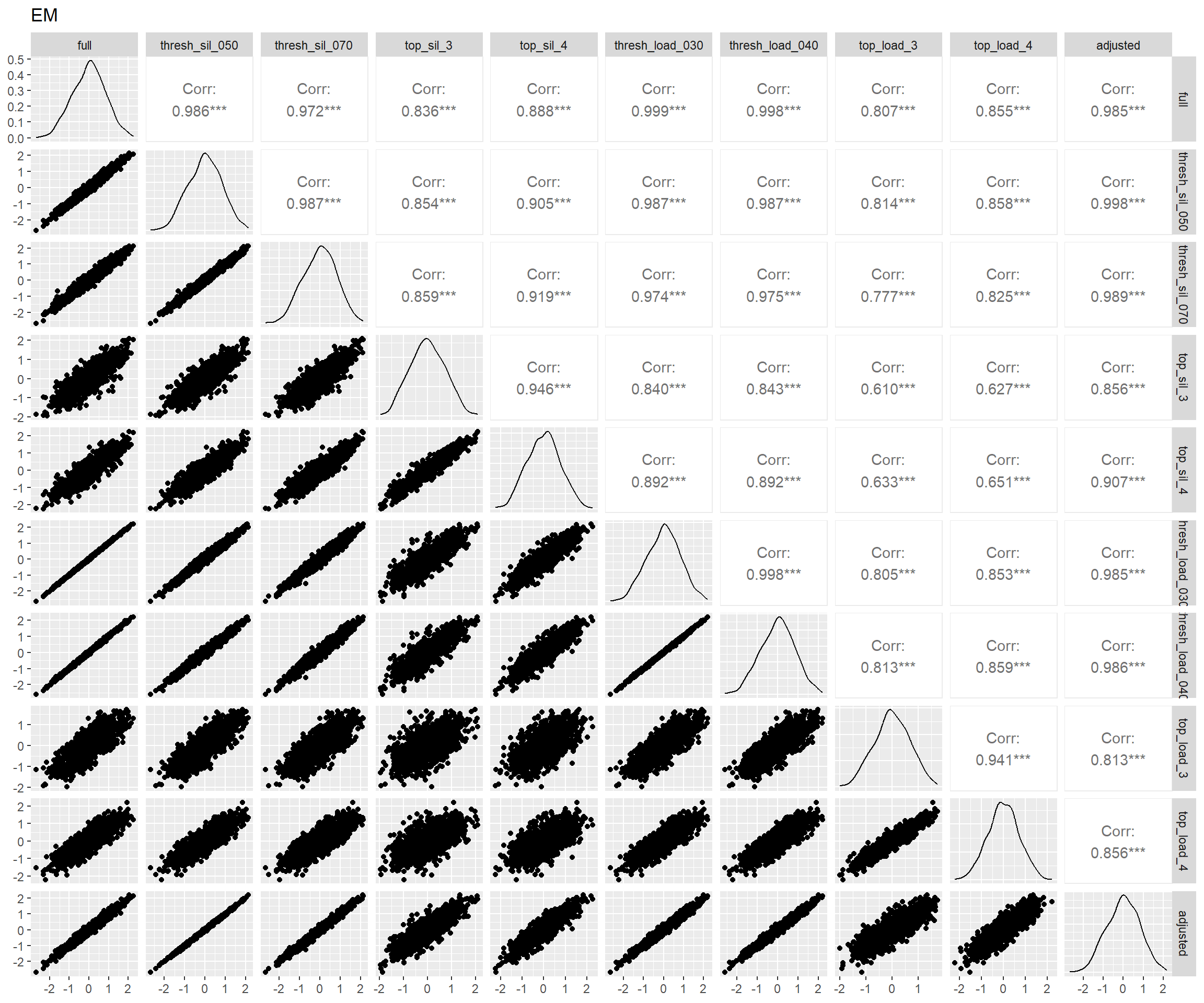
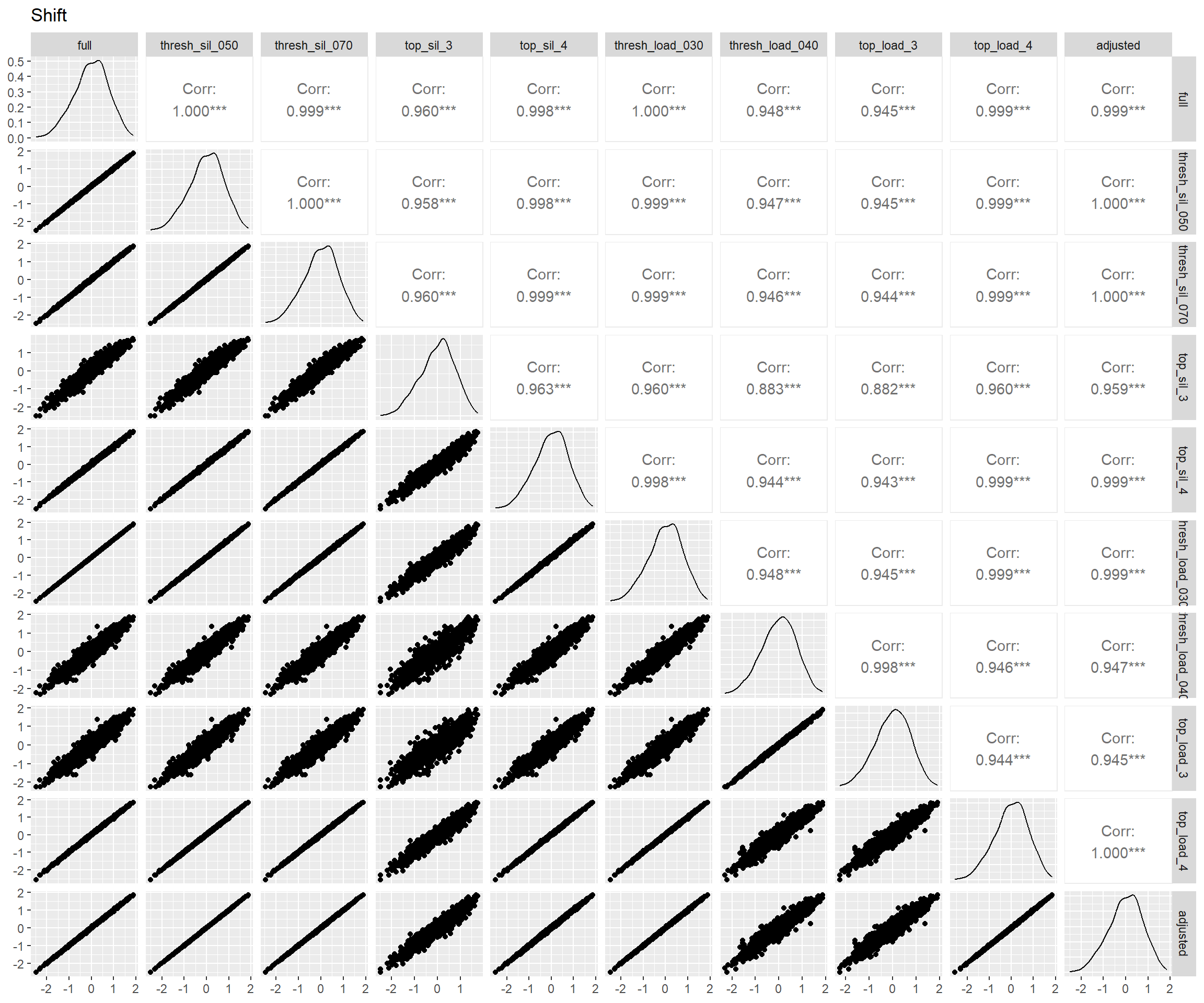
图 7 表明：bi-factor模型和另两个模型拟合出来的特殊能力分数相关仅为0.5上下，这是因为bi-factor模型从这些特殊能力中去掉了一般能力的影响，而另两个模型则一定程度上混入了一般能力(Murray and Johnson 2013)。而bi-factor模型的这一特性正是我们所需要的。

Code 
for (latent in latents) {
  p <- scores_factor |>
    filter(name == "full") |>
    pivot_wider(
      id_cols = user_id,
      names_from = theory,
      values_from = all_of(latent)
    ) |>
    select(!where(anyNA)) |>
    select(!user_id) |>
    GGally::ggpairs() +
    ggtitle(match_dim_label(latent))
  print(p)
}
图 7: 不同理论的因子得分相关

短版本

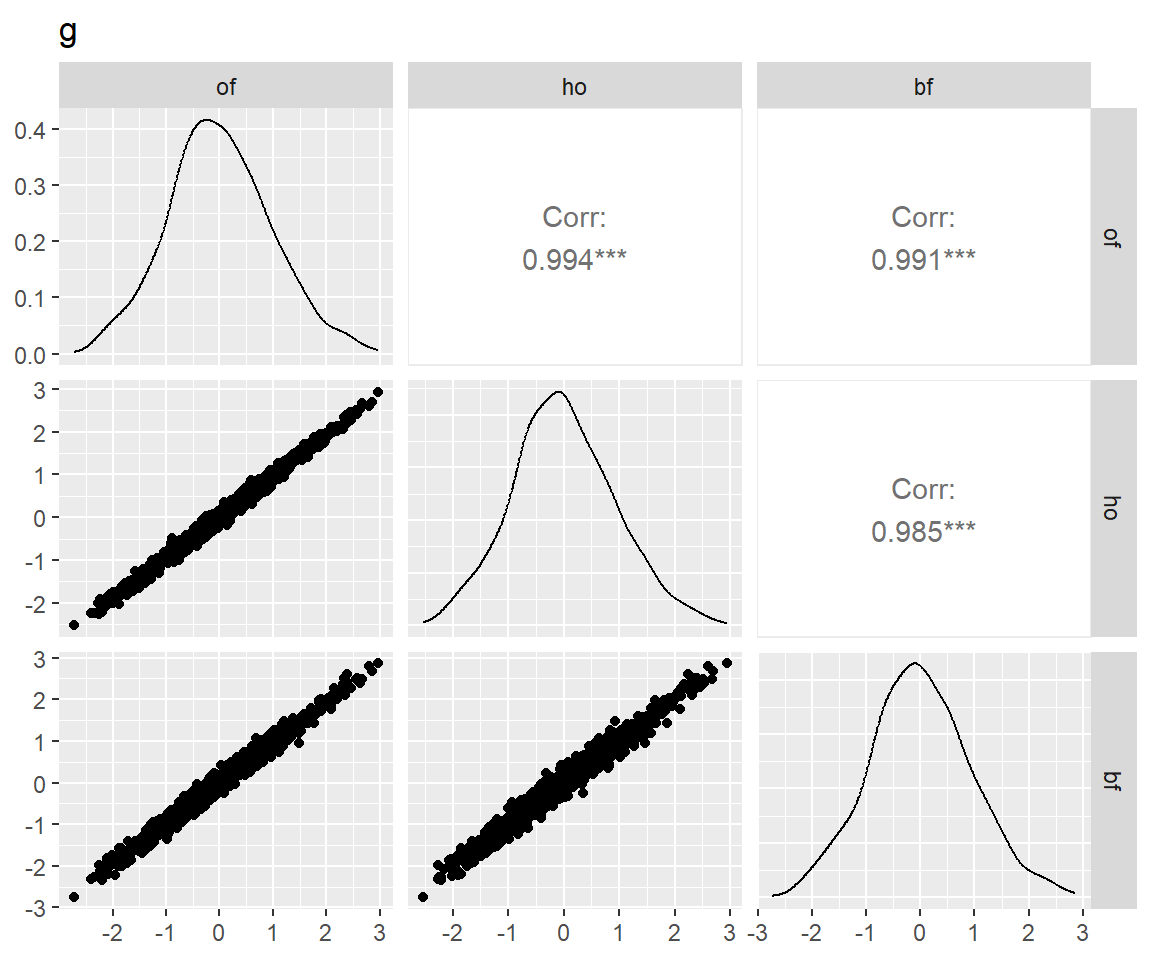
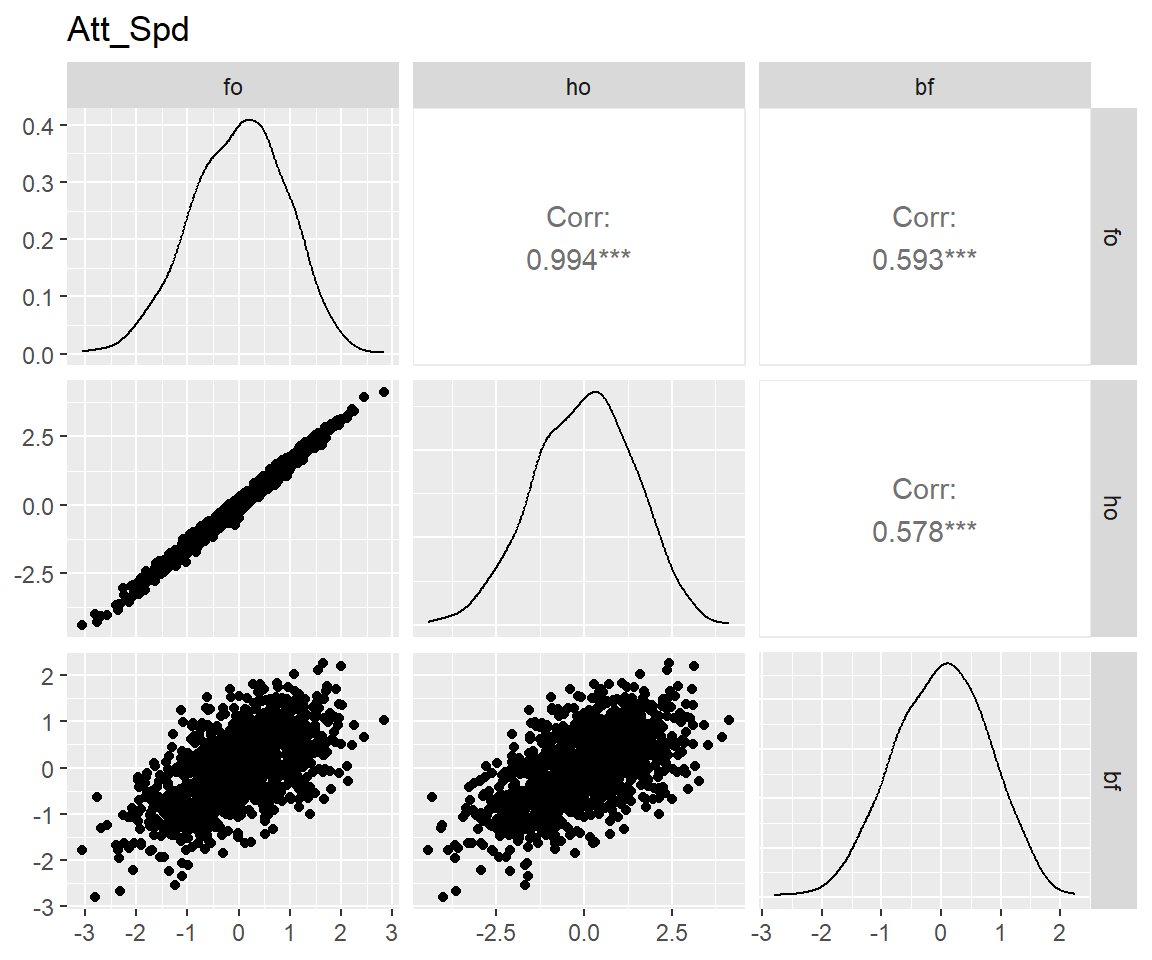
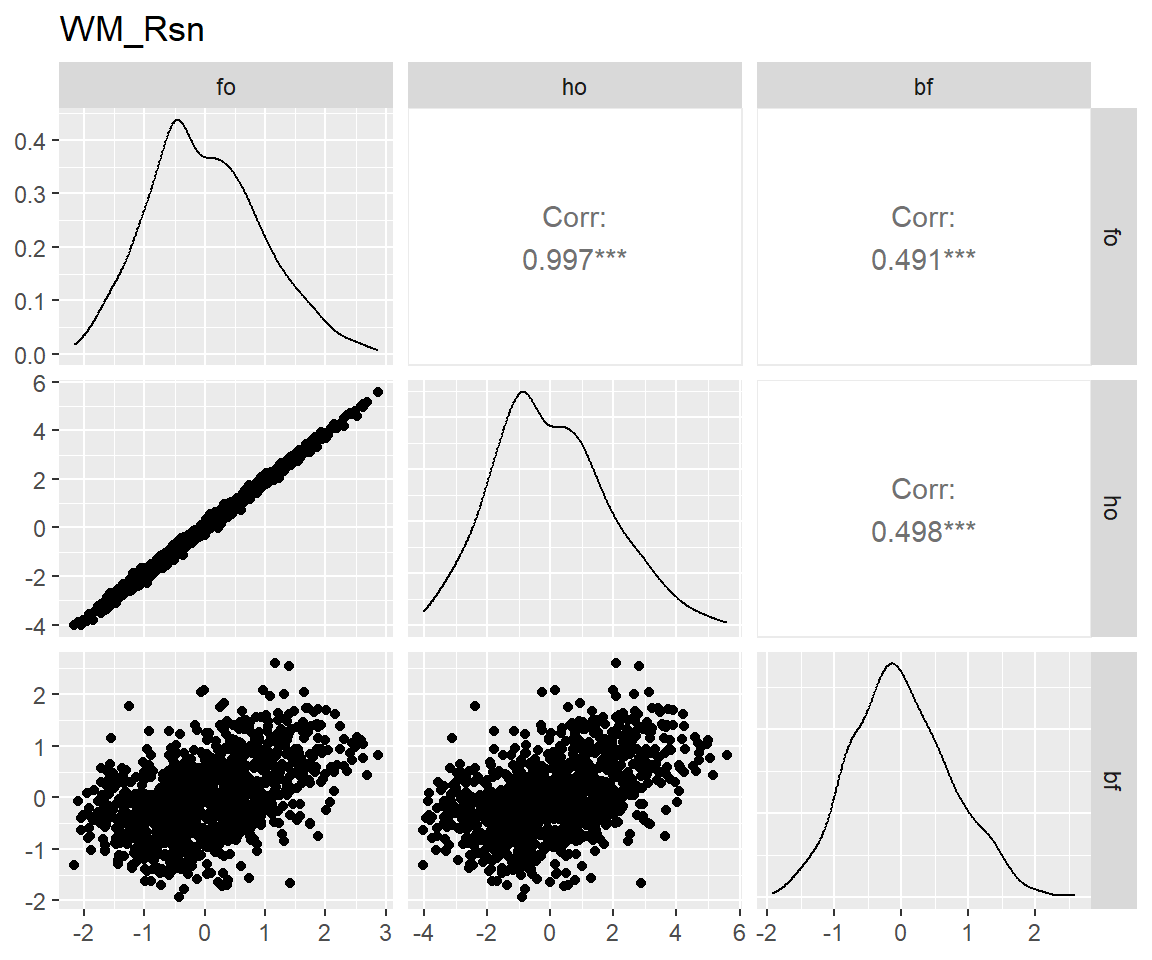
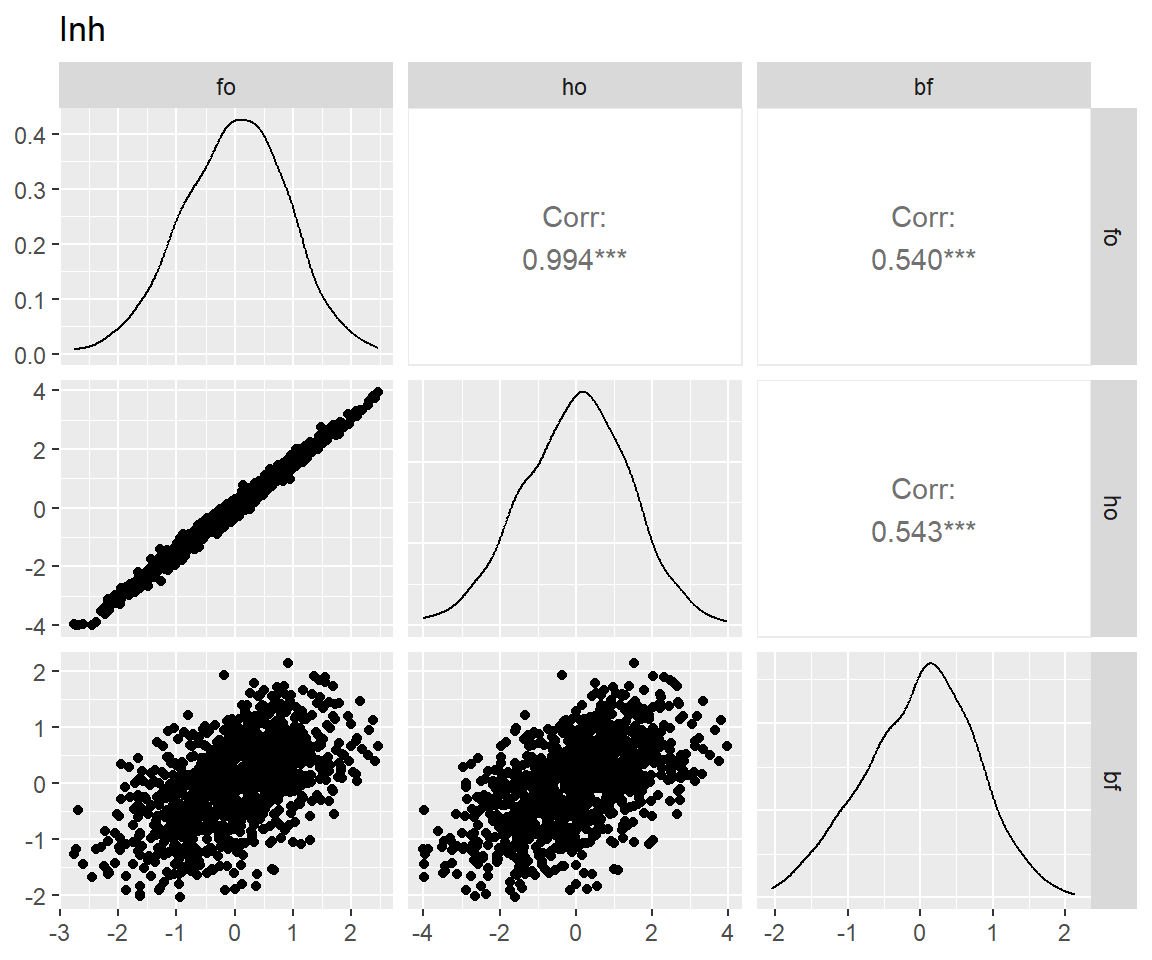
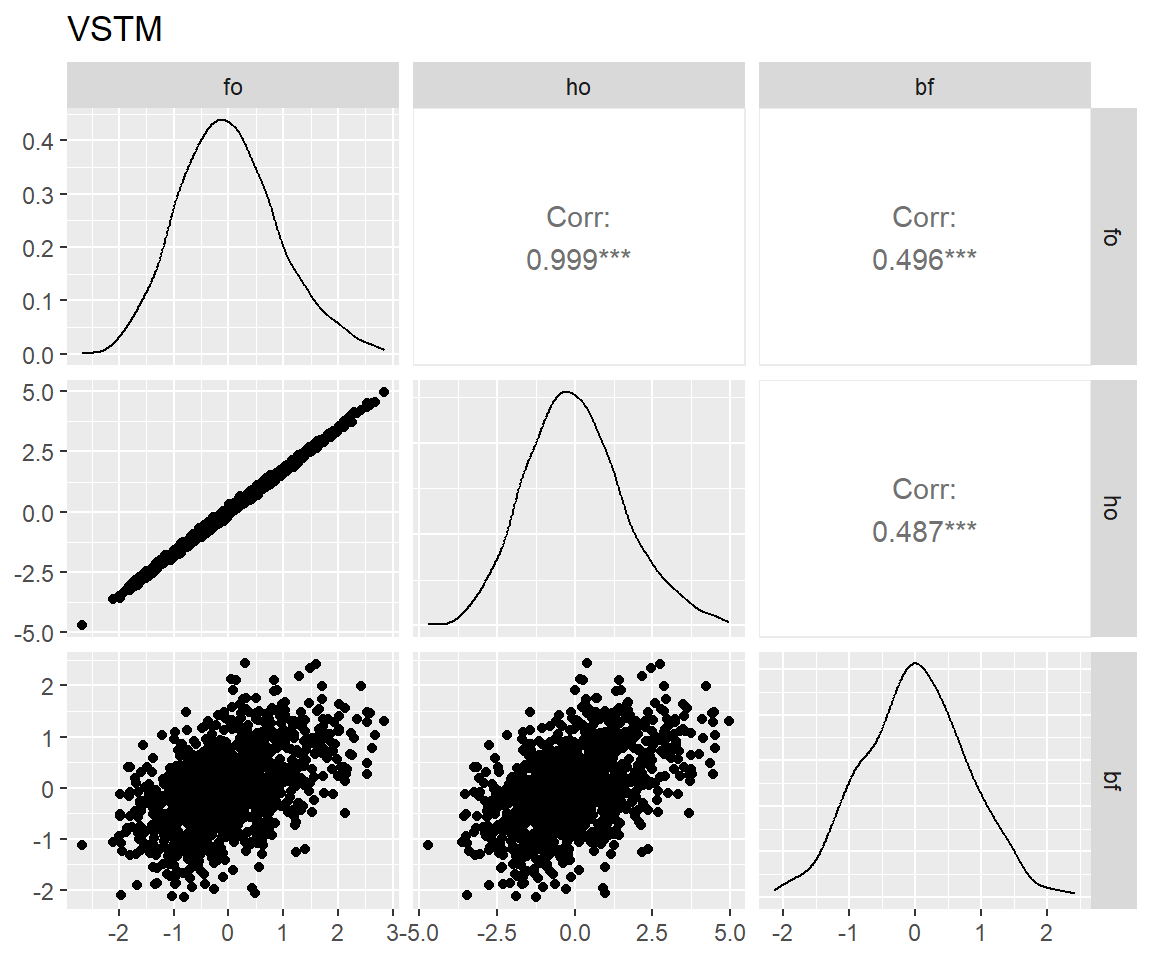
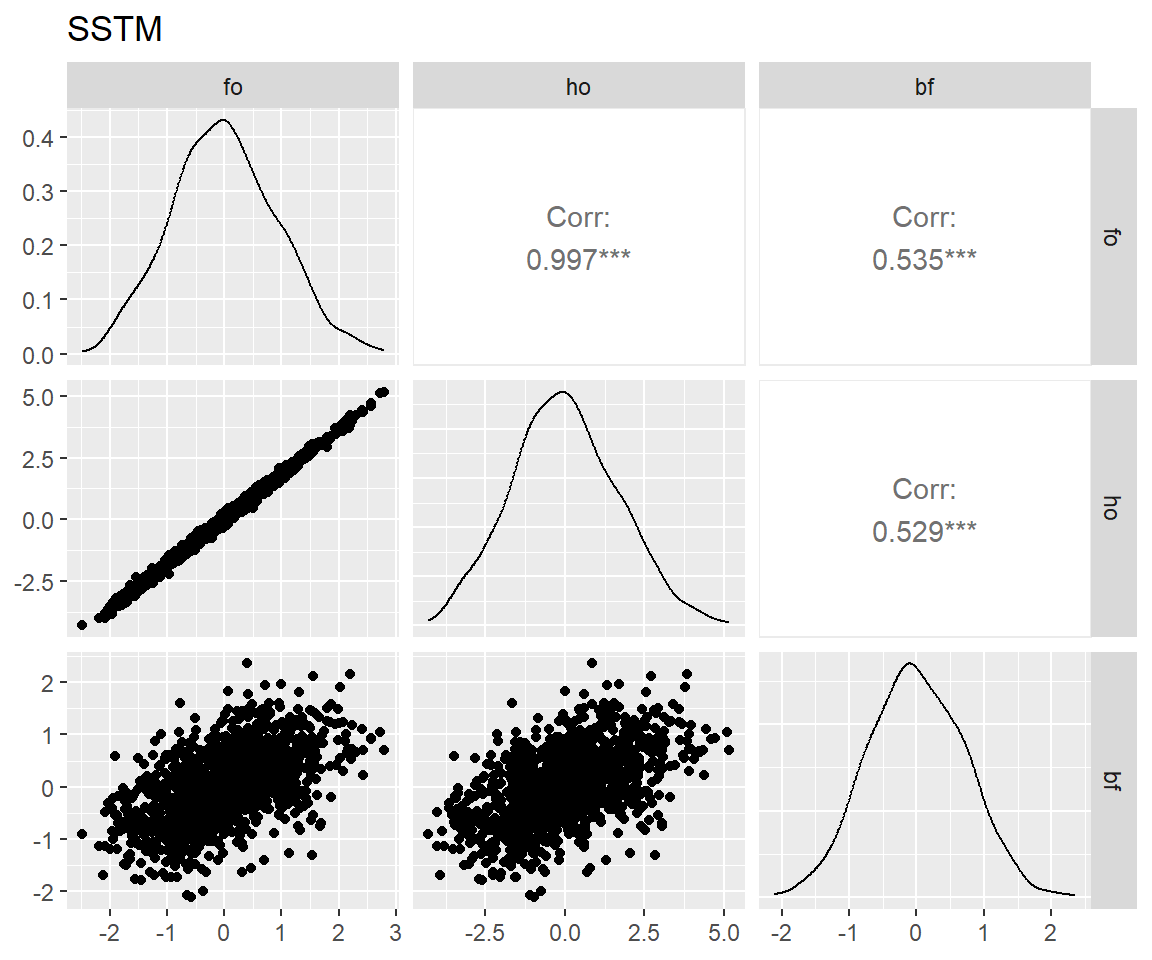
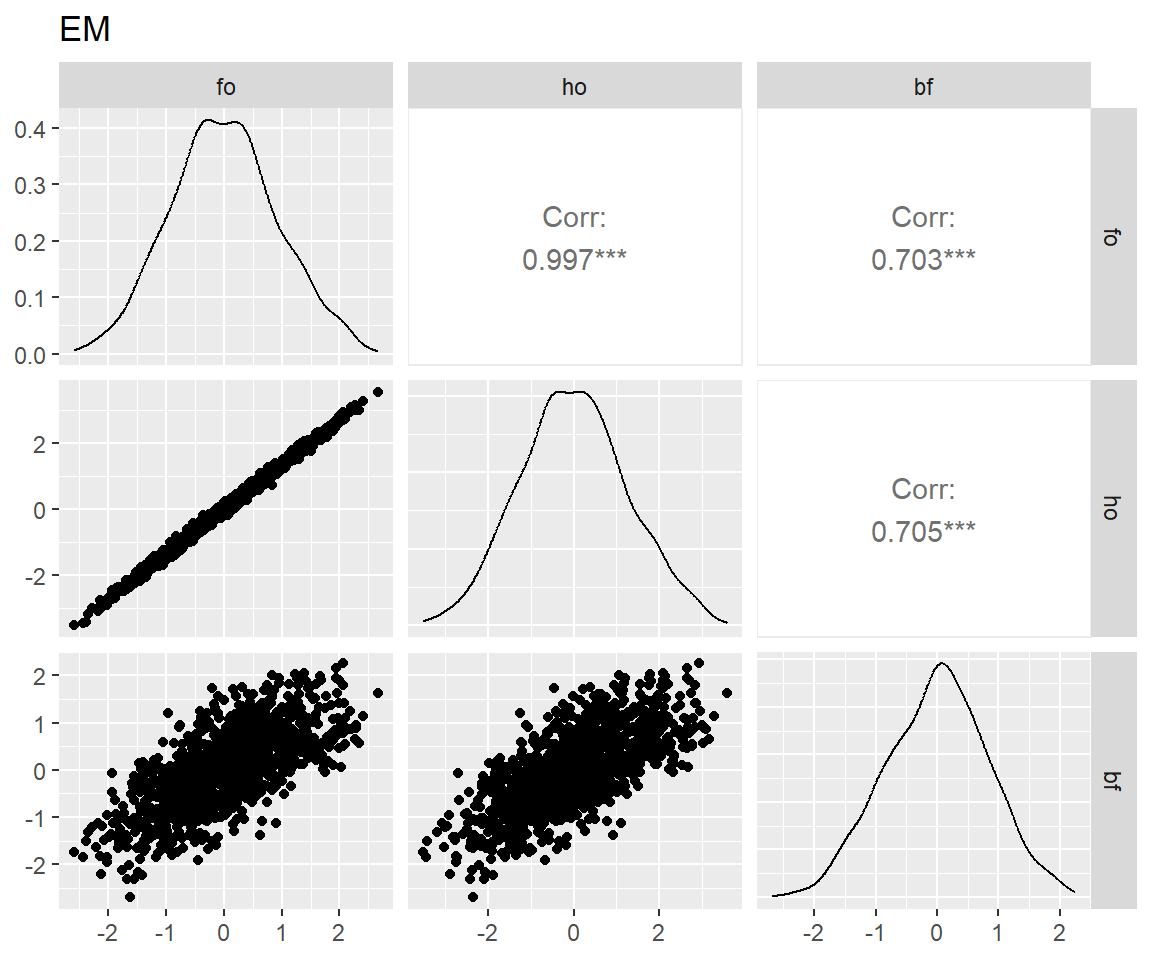
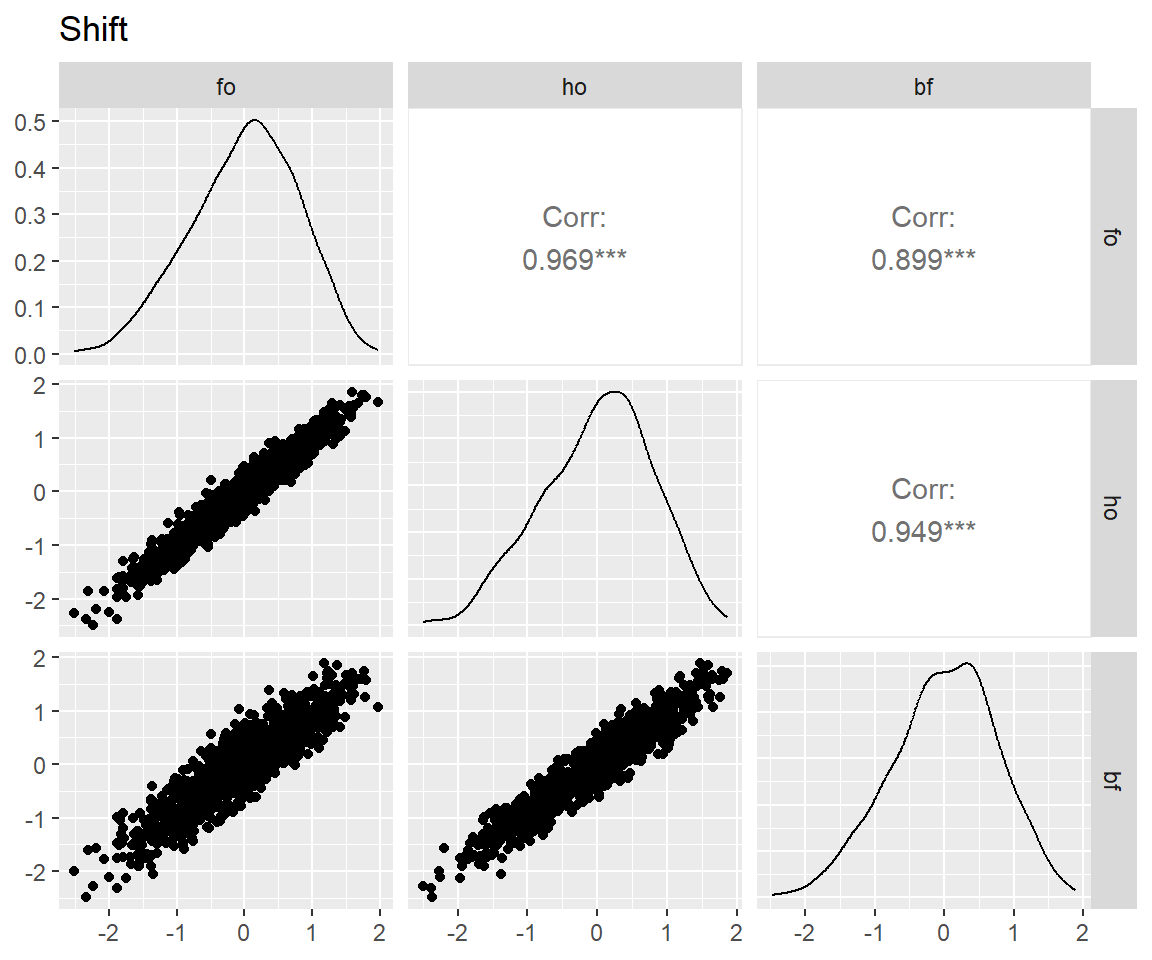
原则：在总时长一样的情况下，如何以最高的准确性测量一般智力和各个子能力维度？

重点比较：

  1. 单一较长版本任务
  2. 多个较短版本任务

References

Murray, Aja L., and Wendy Johnson. 2013. “The Limitations of Model Fit in Comparing the Bi-Factor Versus Higher-Order Models of Human Cognitive Ability Structure.” Intelligence 41 (5): 407–22. https://doi.org/10.1016/j.intell.2013.06.004.
Vuong, Quang H. 1989. “Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses.” Econometrica 57 (2): 307. https://doi.org/10.2307/1912557.

Footnotes

  1. 查看ResearchGate上的一个讨论确定这标准来源。↩︎